Information
Glossary of laser terms
(General notions)
Mode of radiation.
Optical beam quality (M²).
Beam parameter product (BPP).
Spot size.
Depth of focus (DOF).
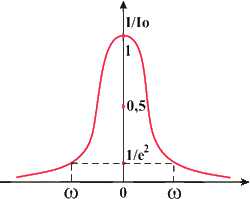
Resonator Mode – the distribution of electro-magnetic field in the cavity, that is reproduced itself during frequent propagation of light wave between resonator mirrors. Industrial lasers radiate usually the superposition of several lowest modes. The basic mode TEM00 does have a Gaussian intensity distribution:
where I – intensity of field, r – radial coordinate, ω – beam radius, measured as a distance where the intensity falls in e² times as compare as the value on the axis I = Io × e ‾ ² (Fig. 1.)
 |
 |
| Fig.1. Gaussian intensity distribution. |
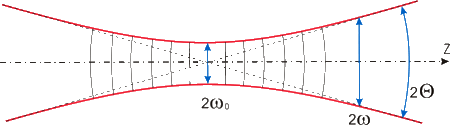
Fig.2. Gaussian beam propagation in empty space. |
By definition, half angle of Gaussian beam divergence is equal:
Where ωo– is the radius of beam waist (Fig.2), λ- is the laser wavelength, π =3,14
The real radius of laser beam (mode radius) is larger than that of theoretical (ideal) ТЕМ00 mode. The real divergence of laser radiation is differ from that of ideal Gaussian beam.
The main reasons which give rise to difference of output laser beam from Gaussian one:
- The shape of laser beam can be non-gaussian for unstable resonators.
- Multi-mode beams can originate in resonators having insufficient selective properties.
- Imperfections of optical elements.
- Thermodeformations of optical elements.
- Thermal lenses which can arise in active medium.
- Non-uniformity of gas density (in fast-flow gas lasers).
One can define a dimensionless beam-quality parameter M2 as a difference of real laser beam divergence from Gaussian beam one as: M²:
M2= Θreal./Θgauss.= Θ/Θ0 (2)
Note, each measurement is done on the 0,86 level of laser intensity, i.e. corresponds to 1/е².
Beam parameter product (BP) is defined as a product of beam waist and half angle of divergence.
Θ×do ≡ "BP"
For Gaussian beam: Θo×ωo =λ/π
Obviously, this parameter is not a constant for real laser beams. This number describes the “quality” of beam propagation, i.e.:
Θ×do =M2λ/π (3)
As follows from abovementioned, the closer the divergence of real laser to diffraction limit, the higher is it's optical quality, and the less "M²" is differ from 1, i.e. М²=1 for TEM00.The formula (3) can be written as:
M2=(π/4λ)×(2do×2Θ),
where 2do – beam diameter is in millimeters and 2Θ – full angle divergence is in milliradians. Both parameters are measured at the level of 1/е². For λ=10,6 µm (CO2 laser):
M2=0,074×(2do×2Θ),
Note, the optical beam quality of radiation for slab lasers was investigated in detail in our published papers .
In practice, smaller focal spot diameter D can be achieved on the workpiece, resulting in greater material penetration for the same laser power. It is useful to know the dependence of D on the lens focal length f, beam diameter 2d on the lens and beam optical quality М²: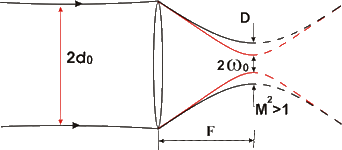
Fig. 3. Parameters of a real laser beam with M2>1 and Gaussian beam
at passing through a focusing lens
D=4λM2f/(π×2d)For CO2 laser:
D=13,5×10-3×M2×f/2d
Here, f, 2d and D are measured in millimeters.
The depth of focus (DOF) can be increased, dependent on machine design details. Expressed in terms of the focal spot diameter, which the operator usually specifies, we have for CO2 laser:
DOFco2=148×D2/M2,
here DOF and D in millimeters. Note, within the DOF the power density on the workpiece material is not less at half of that in focal point.